Full vs. Limited Configuration Interaction

Configuration Interaction (CI) methods begin by noting that the exact wavefunction Ψ cannot be expressed as a single determinant, as Hartree-Fock theory assumes. CI proceeds by constructing other determinants by replacing one or more occupied orbitals within the Hartree-Fock determinant with a virtual orbital.

In a single substitution, a virtual orbital, say φa, replaces an occupied orbital φi within the determinant. This is equivalent to exciting an electron to a higher energy orbital.

Similarly, in a double substitution, two occupied orbitals are replaced by virtual orbitals: φa ← φi and φn ← φj; for example, Ψia = | φ1, … φi, φa+1, … φi-1, φa, … φn|. Triple substitutions would exchange three orbitals, and so on.

Full Configuration Interaction

The full CI method forms the wavefunction ψ as a linear combination of the Hartree-Fock determinant and all possible substituted determinants:

$\psi = b_0 {\psi}_0 + \sum\limits_{s>0} b_s {\psi}_s$

where the 0-indexed term is the Hartree-Fock level, and s runs over all possible substitutions. The b’s are the set of coefficients to be solved for, again by minimizing the energy of the resultant wavefunction.

At a physical level, this equation represents a mixing of all of the possible electronic states of the molecule, all of which have some probability of being attained according to the laws of quantum mechanics. Full CI is the most complete non-relativistic treatment of the molecular system possible, within the limitations imposed by the chosen basis set. It represents the possible quantum states of the system while modelling the electron density in accordance with the definition (and constraints) of the basis set in use. For this reason, it appears in the rightmost column of the following methods chart:

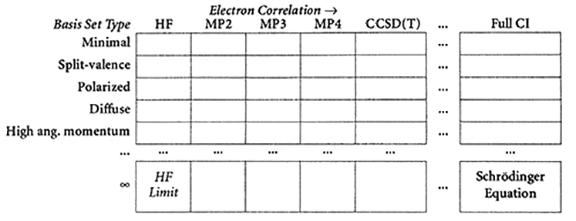
models

As the basis set becomes infinitely flexible, full CI approaches the exact solution of the time-independent, non-relativistic Schrödinger equation.

Limited Configuration Interaction

The full CI method has many of the desirable features of a theoretical model. It is well-defined, size-consistent, and variational. However, it is also very expensive and impractical for all but the very smallest systems.

Practical configuration interaction methods augment the Hartree-Fock wavefunction by adding only a limited set of substitutions, truncating the CI expansion at some level of substitution. For example, the CIS method adds single excitations to the Hartree-Fock determinant, CID adds double excitations, CISD adds singles and doubles, CISDT adds singles, doubles, and triples, and so on.

A disadvantage of all these limited CI variants is that they are not size-consistent. Fortunately, this deficiency is overcome by Coupled Cluster theory. Historically, the Quadratic Configuration Interaction (QCI) method family was said to be constructed to correct this deficiency. For example, QCISD adds terms to CISD to restore size consistency. However, despite descriptions implying a separate origin, QCI methods are based on and completely equivalent to the corresponding Coupled Cluster methods developed earlier (i.e., QCISD is the same as CCSD).