More About Conformational Averaging
Conformational searching is a technique that attempts to locate, for a given molecule, all of the possible distinct potential energy minima that can be interconverted by rotations about formally single bonds. It is as much art as science. It relies on a starting geometry and a list of structural parameters which can be varied in the search for unique conformations. There are a variety of software tools which can perform this task. Different software packages, molecular mechanics force fields, starting structures and/or other parameters will produce differing sets of conformations. In some cases, these differences affect the final predicted properties.
Example 4.8: NMR spectrum of 2,2,4-trimethyl-1,3-pentanediol
In Example 4.8 (beginning on p.164), we predict the NMR chemical shifts with respect to TMS for the carbon atoms in 2,2,4-trimethyl-1,3-pentanediol by performing a conformational search and then Boltzmann averaging the predicted spectra of the compound’s various conformations. In this note, we will discuss some additional practical aspects of conformational searching and the procedure that we followed. Note that the calculations indicated were all performed in the gas phase.
In the example described in the book, we used the Pcmodel package to perform the conformational search, specifically Pcmodel version 10 on a Mac OS X computer. The input file provided for this example in the main input file archive is the starting file for Pcmodel.
Except as noted in the discussion, we used the default values for all settings. In particular, we retained the constraint related to hydrogen bonding which is the default in the software we used (the control is indicated in green below). This had the effect of eliminating structures which do not exhibit hydrogen bonding from our result set. As a result, we located far fewer structures than will be generated by alternate conformational searches.
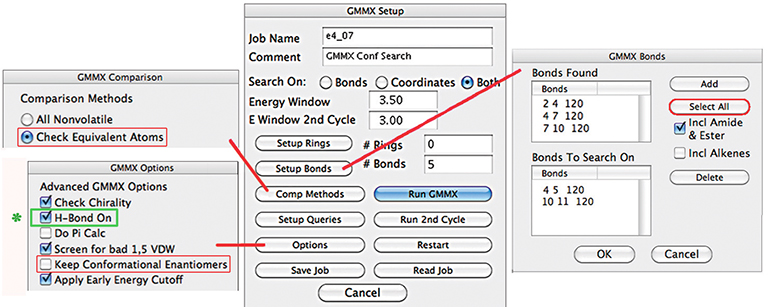
To review, our general procedure included several phases:
- Generate conformations using a software package.
- Optimize those structures in Gaussian using a small basis set (3-21G). Eliminate duplicates.
- Optimize the remaining structures in Gaussian using our standard basis set—6-311+G(2d,p)—and eliminate duplicates.
- Run NMR calculations in Gaussian on the structures which contribute at least ~0.5% to the Boltzmann average. The final weighting factors are calculated after excluding the outlier structures.
- Predict the chemical shift for each carbon atom by Boltzmann-averaging the results of the NMR jobs.
This same study has been completed two additional times using different software for the conformational searching. We are grateful to Dr. Fernando Clemente (Gaussian, Inc.) and Dr. Naofumi Nakayama (Conflex Corp.) for their kind efforts in this endeavor. Two conformational searching software packages were used, both of which are more sophisticated than the version of Pcmodel used in the book: CONFLEX conformational analysis system and a version of an embedded version of Pcmodel contained within visualization software that is still in beta. In both cases, the search used the same MMFF94 force field as we did originally.
The following table summarizes the overall results of the conformational searching and subsequent geometry optimizations:
| # Optimization Jobs | ||||
| Starting Software | # Initial Conformations | small basis set | large basis set | # NMR Jobs |
| Pcmodel 10 | 38 | 38 | 25 | 24 |
| Beta software | 490 | 233 | 199 | 33 |
| CONFLEX | 329 | 329 | 48 | 29 |
Note that both alternate software packages found many more conformations initally; both of these procedures omitted the hydrogen bonding constraint.
Duplicates were removed from the set of initial conformations for the beta software by inspection, resulting in 232 structures. This manual analysis also resulted in the addition of another structure not located by the software.
The procedure using the CONFLEX software eliminated high energy conformations after the first optimization rather than the second, discarding structures whose predicted energy exceeded that of the lowest energy conformer by ~2 kcal/mol or more. The first set of optimizations used the 6-31G(d) basis set rather than 3-21G.
The following table summarizes the predicted chemical shifts for the three procedures:
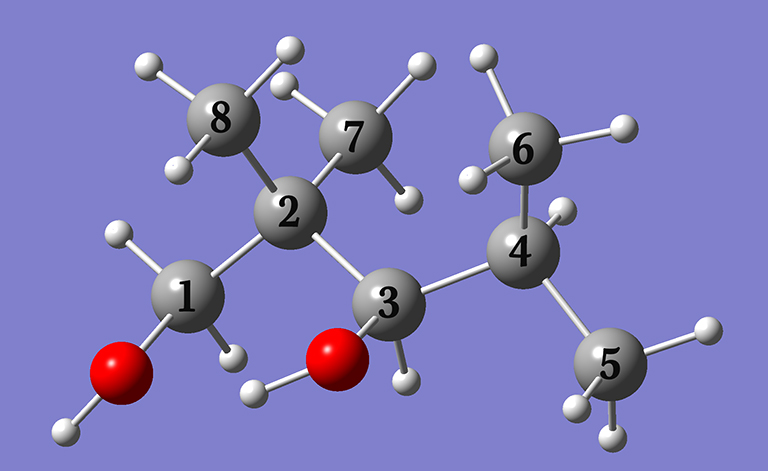
| Starting Software | C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 |
| Pcmodel 10 | 80.64 | 45.99 | 89.50 | 35.27 | 16.54 | 24.54 | 23.98 | 20.70 |
| Beta software | 80.28 | 46.38 | 88.79 | 35.32 | 16.81 | 24.75 | 24.05 | 20.66 |
| CONFLEX | 80.26 | 46.33 | 89.25 | 35.19 | 16.99 | 24.85 | 24.25 | 20.73 |
| Observed | 69.74 | 39.68 | 78.26 | 28.53 | 16.94 | 23.55 | 21.95 | 20.46 |
As the table indicates, the results for the three procedures are very similar. All of them are in reasonable agreement with experiment. In this case, we were fortunate that our inadvertent constraint did not affect the final results. Note that the Pcmodel results here differ from what is in the text (p.169). The table in the book contains a pair of duplicate structures: 9 and 15; structure 9 is removed in the above results.
Click here to download a ZIP archive containing the structure files for this extended discussion of Example 4.8. Note that the carbon center numbering within these jobs differs from that in the table above.
Exercise 7.8: ROA spectrum of aeroplysinin-1
Exercise 7.8 (beginning on p.305) performs a conformational search in order to predict the ROA spectrum of aeroplysinin-1, a molecule with two chiral centers (see the illustration following). The goal of this study is to determine which diastereomer corresponds to the observed spectrum below:
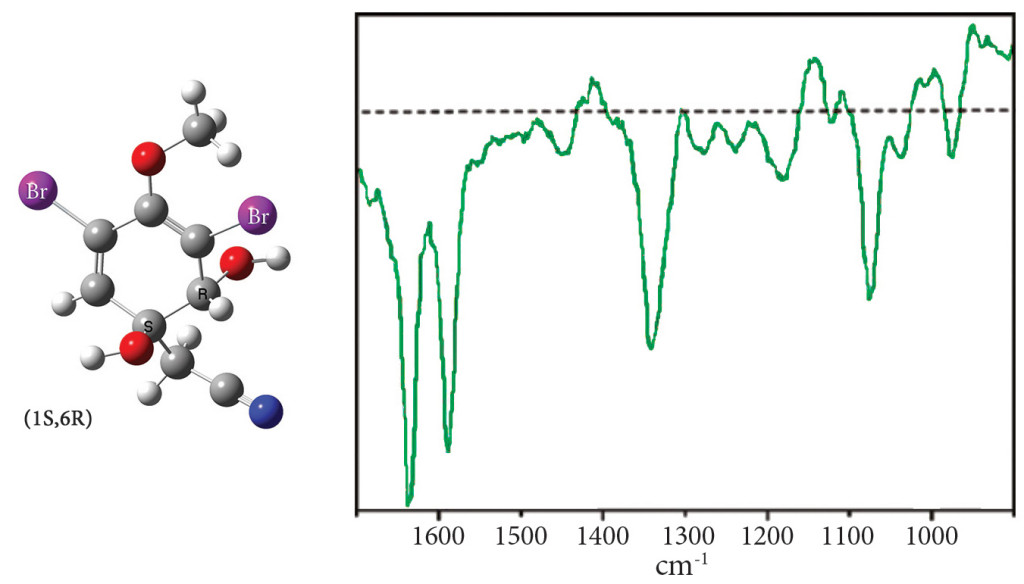
In our study, we explored the conformational space for the (1R,6R) and (1S,6R) diastereomers using the following procedure for each one:
- We scanned the C-C-O-C and C-C-C-C(-N) dihedral angles, in increments of 30°. Each scan located six minima which were then fully optimized. The APFD/6-31G(d,p) model chemistry was used for all jobs.
- A second scan was performed for each optimized minimum over both C-C-O-H dihedrals angles (increment=90°) using the same model chemistry.
- We eliminated duplicate geometries from each set and also discarded ones constituting
less than ~1% of the Boltzmann distribution. We then optimized the remaining structures using our standard model chemistry. - Finally, we ran ROA calculations on the set of optimized structures constituting more than ~5% of the final Boltzmann distribution. Boltzmann averaging of these results produced the final predicted spectrum.
All calculations were performed in aqueous solution.
This procedure was designed to cover the conformation space adequately while keeping the number of calculations to a manageable number for an exercise. Another approach would be to perform a single conformational search of the entire space. Doing so would undoubtedly generate many more Gaussian jobs.
This study was repeated recently by Dr. Fernando Clemente. His procedure differed from ours in two ways:
- The second set of scans used an increments of 120° rather than 90°.
- The criterion used to identify duplicate structures was having essentially identical values for the four key dihedral angles (rather than the predicted energy).
These differences produced different conformation sets at various points in the study. However, the overall results differed only slightly in the end.
The following table summarizes the progress of each study:
| # Structures | ||||
| original study | new study | |||
| Phase | (1R,6R) | (1S,6R) | (1R,6R) | (1S,6R) |
| minima from initial scan | 6 | 6 | 6 | 6 |
| distinct† minima from 2nd scan set | 12 | 34 | 14 | 54 |
| large basis set opts | 11 | 20 | 10 | 19 |
| resulting unique† structures | 11 | 19 | 10 | 19 |
| ROA calculations | 6 | 8 | 6 | 7 |
| †Duplicate criteria: original study: energy; new study: 4 key dihedral angle values. | ||||
The following figure compares the predicted ROA spectra produced by the two studies:
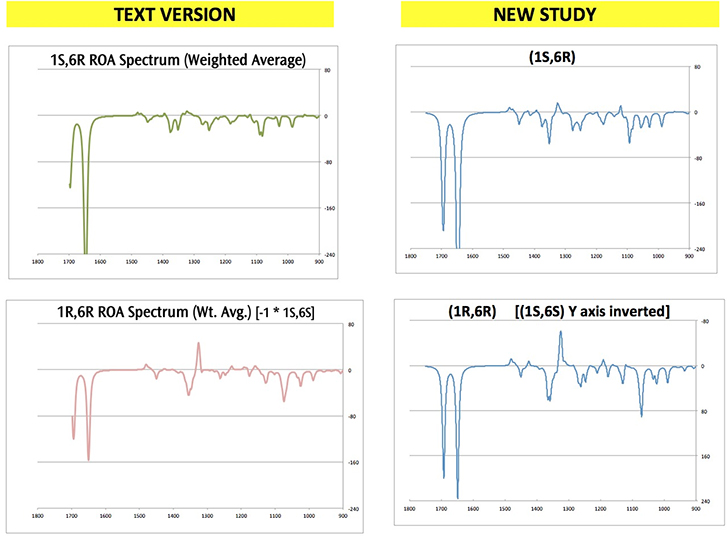
Click here to download a ZIP archive containing the structure files for this extended discussion of Exercise 7.8. Note that diastereomer modeled in some jobs is the chiral opposite of what is discussed in the text (e.g., (1S,6S) instead of (1R,6R).






